Insurance Principles Demonstrated by a Simple Example

Author: Samuel Peterson

Date Published
2017-10-29 (ISO 8601)
72-10-29 (Post Bomb)

Some years ago, I was studying for an actuarial exam which covered financial economics models. While reading through the text which the test was based on, I came across a line that went something like this:

For a given portfolio of stochastically independent exposures to risk, the cost of uncertainty per item approaches 0 as the number of risk exposures increases to infinity.¹

This statement was given without any formal proof or example, and, while it seemed intuitive, I did not have a ready example in mind for which the principle could be shown rigorously. Some days later, when I had time to kill, I decided to construct such an example. The result was interesting enough that I thought I would share it with you. As an aide to the inquisitive layman, I shall include links to the wikipedia pages for certain mathematical entities which might not be common knowledge; I will not, however, include too much in the way of explanation here except for some very simplified explanations and figures.

The Model

Suppose we have N individuals, members of what we will call the risk-pool, each of whom will incur a loss of \(1\) with probability \(p \ll 1\), and \(0\) with probability \(1-p\) at the end of some period of time. Let us further suppose that an expense of \(1\) will bankrupt any individual, but that each individual can easily incur without bankruptcy the expected value of their loss, which in this case is equal to \(p\). Finally let us suppose that the occurrence of a loss for any one individual is statistically independent² from all other individual's losses or lack thereof.

In this case then, the losses of the N individuals can be modeled with by the independent random variables: \(\{X_1, X_2, \dots, X_N\}\), where \(X_i\) represents the loss of the i^th individual, and is governed by the Bernoulli distribution.

Funding the losses

With things as they stand, the probability that someone will be bankrupted due to their risk exposure is \(P_d(N) = 1 - (1-p)^N\). Note that \(\lim_{N \to \infty} P_d(N) = 1\). What can be done to lower the probability of someone defaulting, assuming no one in our risk-pool is altruistic enough subscribe to a relief fund which pays a variable amount equal to the total loss in the pool? One possibility is for each member to pre-pay into a fund the expected value, \(E[X]\), of their own loss. Let's see how that will pan out.

The total amount given to the fund is \(N E[X] = N p\), and the total loss incurred in our risk-pool at the end of a time period is given by: $$ L_N = \displaystyle\sum_{i=1}^{N} X_i .$$ Since \(L_N\) is a sum of \(N\) independent, identically distributed Bernoulli random variables with probability of \(p\), then L has the binomial distribution, with parameters \(N\) and \(p\). The probability of bankruptcy then becomes: $$ P(L > N p) = 1 - \displaystyle\sum_{k=0}^{\lfloor N p \rfloor} \binom {N}{k}p^k (1-p)^{N-k}, $$ Where \(\lfloor x \rfloor\) is defined as the largest integer less than \(x\), \(\binom{n}{t} = \frac{n!}{t!(n-t)!}\) and \(n! = n(n-1)(n-2)\dots(2)(1)\). Depending on the parameters \(N\) and \(p\) this figure will vary, but it will be around \(\frac{1}{2}\).

We're getting there. Keeping the default probability around \(\frac{1}{2}\) is a lot better than being able to count on default for large N. But we can do better. Before we do that however, let us make a digression so we can approximate the probability of default with a much nicer function which you are probably more familiar with: the normal distribution.

Central Limit Theorem

I won't go into much detail about the Central Limit Theorem, but I thought I'd do a little more than just provide a link (and I want to use this excuse to make some figures). The short and sweet of it is this: the distribution of sums of random variables, such as \(L_N\), converge to the normal distribution. Some conditions of the sum must hold in order for this to be true:

• The standard deviation of the summands must be defined
• The standard deviations can't grow too rapidly (This last condition will always be true if the summands are identically distributed and the last condition is satisfied)

For our particular case, the Central Limit Theorem (CLT) would be applied to a scaled and shifted version of our loss variable: $$ \tilde{L_N} = \frac{L_N - Np}{\sigma_N}, $$ where \(\sigma_N\) is the standard deviation of of \(L_N\). The CLT states that \(\tilde{L_N}\) converges to the normal distribution of mean 0 and standard deviation of 1, which is called the standard normal distribution. The speed of the convergence is demonstrated in the following figure.

As you can see, the CLT gives us a good approximation of the distribution of our transformed loss, \(\tilde{L_N}\), for N greater than 1000 or so in the case of \(p = .05\). We will use this approximation for our our future analysis, with the understanding that it is valid insofar as the standard normal distribution is a good approximation of \(\tilde{L_N}\).

Funding the loses (continued)

Picking up where we left off before our digression on the CLT, we see that if each member of the risk-pool pays the expected value of their loss, p, then the insurance fund will have enough to cover all losses in a given period with probability around \(\frac{1}{2}\). How do we improve on that probability? The obvious solution is for each member to pay an additional amount. Suppose now that each member pays \(p + \delta\) where \(\delta > 0\) is the risk premium. What does that extra fee get us?

The money contributed to the fund is now \(N(p + \delta)\), and our total loss at the end of the period is still \(L_N\). Before we look at the probability that the fund is bankrupted, a useful thing to know will be that \(\sigma_N\), the standard deviation of \(L_N\), is given by $$ \sigma_N = \sqrt{Np(1-p)}. $$ Note that \(\sigma_N\) grows at the rate of \(\sqrt{N}\) (as opposed to N). This is due to the \(X_is\) being independent, and it will be a useful property.

With that out of the way, we see that the probability of bankruptcy of the fund is given by: $$ \mathbb{P}(\text{bankruptcy}) = \mathbb{P}( L_N > N(p + \delta)) = 1 - \mathbb{P}( L_N \le N(p + \delta)) $$ $$= 1 - \mathbb{P} ( \frac{L_N - Np}{\sqrt{Np(1-p)}} \le \frac{N\delta}{\sqrt{Np(1-p)}} ) .$$ Observe the argument for the probability function in the last equality: the left hand side of the inequality is just \(\tilde{L_N}\) from the section above, whose distribution can be approximated with the standard normal, Z. Note too that on the right hand side of the inequality, the \(N\) in the numerator is only partly cancelled out by the \(\sqrt{N}\) in the denominator. The end result of the above is the following: $$ \mathbb{P}(\text{bankruptcy} = 1 - \mathbb{P}( Z \le \frac{\sqrt{N} \delta}{\sqrt{p(1-p)}}). $$ This quantity converges to 0 for any \(\delta > 0\), no matter how small. Note however, that for a smaller \(\delta\) the probability of default decreases at a slower rate. It is in this sense that the cost of uncertainty goes to zero as N approaches infinity. The principle can perhaps be better illustrated with a somewhat different question: "If my risk pool is of size \(N\) and I want the probability of default to be no larger than q, how small can my risk premium, \(\delta\) be?" The answer can be demonstrated with the following figure which graphs the answer vs. N, with \(p = q = .05\).

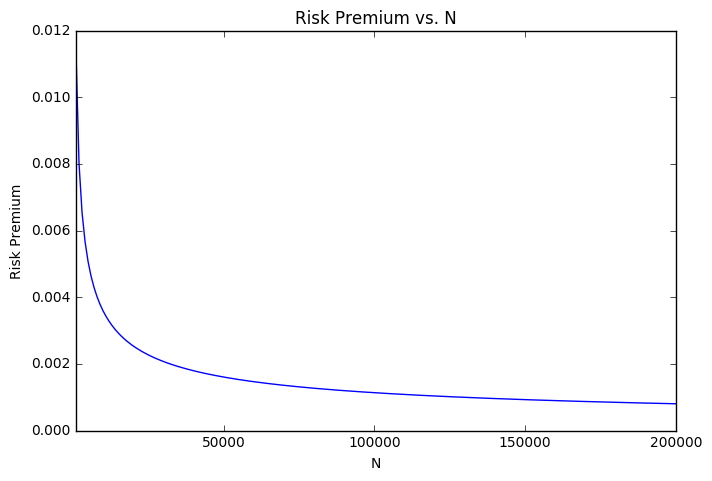
Final remarks

You probably wouldn't be surprised that the actual practice of insurance pricing is much more complicated, but there are some principles illustrated here that apply regardless of the intricacy of the methods involved:

• There's no free lunch: collective financial security cannot get people out of paying the expected value of loss
• Uncertainty becomes cheaper with a larger risk pool. In our example this is due to the standard deviation growing like \(\sqrt{N}\), while gross risk-premium income grows like \(N\). Statistical independence of items in the risk-pool is necessary for this behaviour to arise. As risks become more correlated, the efficacy of this funding strategy breaks down. So if the Avengers assemble in New York, it's likely your insurance company is going to run into trouble.

So if a larger risk-pool is better, why isn't there just one global insurance policy? Different companies exist for two reasons. The first is competition: competitors in the insurance realm compete over that risk-premium, which can vary based on the risks the insurance firm is willing to take on themselves, and on the refinements of the models which estimate the cost of uncertainty. The second reason is specialization: models for different kinds of risk exposures vary greatly and involve specific expertise: automobile risk behaves differently from health risk, financial risk, or large-scale casualty risk; since companies compete at least partly based on their ability to finely model the risks in a given portfolio, expertise in certain niches is a natural consequence.

That being said, in a sense there is just one risk-pool. Most, if not all, insurance companies are themselves insured by reinsurance firms, who pay out claims in case of massive loss. Since a given reinsurance firm has risk portfolios from many different insurance firms, the result is that the individual risk-pools of the different firms are loosely coupled, which in turn results in a further reduction in the probability of bankruptcy -- exactly what one gets from an increase in the risk-pool.

1: I am sure this is not an exact quotation, but the idea was the same.

2: If you don't want to consult wikipedia, we can think of each loss as the result of a flip of an unfair coin, where heads is flipped with probability p, and tails with probability 1-p. The independence is just a way of saying that each individual flip of the coin is not effected by the result of any other flip.